Intro Logistic Regression,逻辑回归,实质上解决的是一个分类问题 (我们之前说过,机器学习主要解决两类问题:回归和分类)。那为什么它又叫Regression呢?这是因为它用到了一个非线性函数——sigmoid函数 ,它给出的结果是一个概率值,而不是一个用于直接确定分类的离散值。下面我们就来仔细看看这个非常常用的分类算法。
原理 首先我们还是基于传统的线性回归(Linear Regression)去思考一个分类问题,假设我们的模型预测值是,这个值的范围是不确定的,我们很难去找到一个不错的阈值去划分两类(因为模型的输出会受数据分布的影响,0.5并不是一个很科学的阈值)。这个时候我们就需要将的值压缩到一个相对小的区间中,最理想的情况就是压缩到[0,1]中,这样输出的就可以是一个概率了。
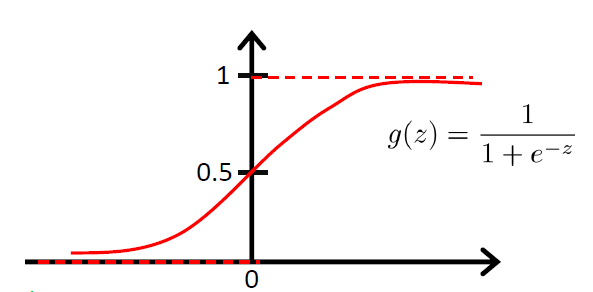
幸运的是,我们能找到这样的函数——Sigmoid function (Logistic function)。它的曲线是这样的:
从sigmoid的图像中我们可以看到一些我们想要的特性:
当时,;当时,
的值被限制在了[0, 1]
sigmoid是光滑的,他的导数也是很容易求得:
于是模型的输出就变为:
最大似然法的思路是:我已经知道了若干个测试结果,我需要找出一组参数,使得它们能够很好地模拟出这些测试结果。将每一个模拟的概率乘起来,极大化这个概率,我们就能得到最好的。下面我们就来表示这些概率。
首先我们假设:
至此,Logistic Regression的原理推导就完成了!大家最好能够自己手动推导一次。
实战 这里我用逻辑回归来预测疝气病马的存活问题。数据集来自UCI:传送门
数据预处理 之前的博客给过处理UCI数据的一些代码模板,需要特别注意,这次的数据存在许多缺漏,因此我们需要手动处理一下。
这里也简单地介绍一下如何处理缺失数据。处理缺失数据是特征工程一个很重要的部分,因为随便填补或删除会使得数据有可能加入了人为的噪声,所以我们需要有多种方法去填补。以下是几个典型的方法:
使用可用特征的均值(或众数)来填补缺失值;
使用特殊值来填补缺失值,如-1(相当于添加了一个新的类别)
直接忽略掉有缺失值的样本(对于缺失属性较多的样本可以这样做)
使用相似样本的均值填补缺失值
使用其他机器学习的方法预测缺失值(如使用随机森林来预测,相当于根据已知特征来预测缺失的特征)
对于这个样本,我的处理主要有两个:
使用0来填补缺失值,因为0对回归系数不会有影响,不会添加人为的bias。
如果某个样例的标签(label)缺失,则直接丢弃这个样例。(相当于不知道答案就不用做题)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 import numpy as npfrTrain = open ('./horse_colic_data.txt' ) frTest = open ('./horse_colic_test.txt' ) trainSet=[] for line in frTrain.readlines(): currLine=line.strip().replace('?' , '0' ).split('\t' ) temp = currLine[0 ].split(' ' ) lineArr=[] for i in range (22 ): if i == 2 : continue else : lineArr.append(float (temp[i])) if (temp[22 ] == '1' ): lineArr.append(1 ) else : lineArr.append(0 ) trainSet.append(lineArr) trainSet.pop(132 ) print(type (trainSet)) np.savetxt('processedHorseColicTraining.txt' , trainSet, fmt='%.6f' , delimiter='\t' ) testSet = [] for line in frTest.readlines(): currLine=line.strip().replace('?' , '0' ).split('\t' ) temp = currLine[0 ].split(' ' ) lineArr=[] for i in range (22 ): if i == 2 : continue else : lineArr.append(float (temp[i])) if (temp[22 ] == '1' ): lineArr.append(1 ) else : lineArr.append(0 ) testSet.append(lineArr) np.savetxt('processedHorseColicTest.txt' , testSet, fmt='%.6f' , delimiter='\t' )
构建Logistic回归分类器 定义sigmoid函数,使用梯度上升法求解。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 from numpy import *import pandas as pdimport numpy as npdef loadDataSet (): file = './processedHorseColicTraining.txt' df = np.loadtxt(file) dataMat = df[:, 0 :-1 ] labelMat = df[:, -1 ] return dataMat, labelMat dataMat, labelMat = loadDataSet() print(dataMat.shape) def sigmoid (x ): return 1 /(1 +exp(-x)) def gradientAscent (dataMatIn, classLabels ): m,n=shape(dataMatIn) print(n) classLabels = np.array([classLabels]).T weights = np.ones((n,1 )) alpha = 0.001 max_iter = 500 for _ in range (max_iter): h = sigmoid(np.dot(dataMatIn, weights)) error = classLabels - h weights += alpha * np.dot(dataMatIn.T,error) return weights
随机梯度上升法 这里试用随机梯度上升法,每次梯度更新仅用到了一个样例。
1 2 3 4 5 6 7 8 9 def stochasticGradientAscent (dataMatIn, classLabels ): m, n = np.shape(dataMatIn) alpha = 0.01 weights = np.ones(n) for idx in range (m): h = sigmoid(sum (dataMatIn[idx] * weights)) error = classLabels[idx] - h weights += alpha * error * dataMatIn[idx] return weights
构建输出部分 前面提到,Logistic Regression的输出是一个概率值,我们需要将这个概率值转化为一个类别,用0.5作为阈值是一个不错的选择。
1 2 3 4 5 6 def classifyVector (inX, trainWeights ): prob = sigmoid(sum (np.dot(inX,trainWeights))) if prob > 0.5 : return 1 else : return 0
测试 使用测试集来评估模型的效果。同时还可以对比两种不同的梯度上升法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 test_file = './processedHorseColicTest.txt' df_test = np.loadtxt(test_file) testDataMat = df_test[:, 0 :-1 ] testLabelMat = df_test[:, -1 ] print(testDataMat) import timestart = time.clock() result2 = advancedStochasticGradientAscent(dataMat, labelMat, 500 ) end = time.clock() print (end - start)errorCount = 0 ;numTestVec = 0 ; [rows, cols] = testDataMat.shape for i in range (rows): numTestVec += 1 if classifyVector(array(testDataMat[i, :]), result2) != int (testLabelMat[i]): errorCount += 1 print(errorCount, numTestVec) errorRate = (float (errorCount) / numTestVec) print('the error rate of this test is: %f' % errorRate)
测试结果:
使用Sklearn 使用Sklearn构建LogisticRegression模型非常简单,只需要定义几个变量就可以了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 from sklearn.linear_model import LogisticRegressionimport numpy as npdef colicSKlearn (): file = './processedHorseColicTraining.txt' df = np.loadtxt(file) dataMat = df[:, 0 :-1 ] labelMat = df[:, -1 ] test_file = './processedHorseColicTest.txt' df_test = np.loadtxt(test_file) testDataMat = df_test[:, 0 :-1 ] testLabelMat = df_test[:, -1 ] classifier1 = LogisticRegression(solver='liblinear' , max_iter=20 ).fit(dataMat, labelMat) classifier2 = LogisticRegression(solver='sag' , max_iter=5000 ).fit(dataMat, labelMat) test_accuracy = classifier1.score(testDataMat, testLabelMat) * 100 print('Accuracy: %f%%' % test_accuracy) if __name__ == '__main__' : colicSKlearn()
这里简单解释一下模型的参数:
solver:优化算法。选项为:
liblinear:坐标下降法lbfgs:拟牛顿法,使用二阶导数来优化(海森矩阵)。newton-cg:牛顿法的一种。sag:随机平均梯度下降saga:SAG的加速版本
测试的结果正确率为73.529412%,似乎比我们自己写的要好一点点。
总结 Logistic Regression是机器学习中分类算法的基础,应用的范围非常广,实际效果也非常不错。一定要注意区分它和线性回归,它的数学原理推导部分是重点!至于实际应用,调用sklearn的模型就可以了。


v1.5.2