LMS--最小均方法

Intro

最小均方法，Least Mean Square（简称LMS），是一种通过最小化误差的机器学习算法。它是机器学习常用的算法之一，通常结合梯度下降法来求解出最优的参数。

LMS算法

loss function

所谓均方，就是误差的平方的均值。LMS训练法则，可以简述为以下式子，通常也叫做代价函数（cost function）：
$J (w) = \frac{1}{2} \sum_{i = 1}^{m} {h (x^{(i)}) - y^{(i)}}^{2}$
其中， $h (x^{(i)})$ 为学习网络的输出信号， $y^{(i)}$ 为导师信号。

Gradient Descent

我们的目的就是要通过某种方法，来最小化这个代价函数。通常使用的方法是梯度下降法（gradient descent），因为对于凸优化问题而言，导数值为0的地方就是全局极小值。所以我们可以利用梯度来指引我们向极小值处走近。

梯度下降法的更新规则为：
$θ_{j} := θ_{j} - α \frac{\partial}{\partial θ_{j}} J (θ)$
**注意:**这里的 $θ_{j}$ 的更新是同步的（即是用相同的 $J (θ)$ ），也就是说，更新完所有的 $θ_{j} （ j = 0, \dots, n ）$ 后，才算下一个梯度。

然后我们推导梯度的计算：
$\begin{aligned} \frac{\partial}{\partial θ_{j}} J (θ) & = \frac{\partial}{\partial θ_{j}} \frac{1}{2} (h_{θ} (x) - y)^{2} & = 2 \cdot \frac{1}{2} (h_{θ} (x) - y) \cdot \frac{\partial}{\partial θ_{j}} (h_{θ} (x) - y) & = (h_{θ} (x) - y) \cdot \frac{\partial}{\partial θ_{j}} (\sum_{i = 0}^{n} θ_{i} x_{i} - y) & = (h_{θ} (x) - y) x_{j} \end{aligned}$
因此对于某一个样例来说，其更新规则为：
$θ_{j} := θ_{j} + α (y^{(i)} - h_{θ} (x^{(i)})) x_{j}^{(i)}$
可以看出，当预测值 $h_{θ} (x^{(i)})$ 和真实值 $y^{(i)}$ 相等时，该参数并不会更新；而当它们不相等时，参数会按照他们的difference来更新参数，这样从直观上来说也是合理的。

梯度下降法给我们提供了一种求代价函数极小值的方法，它有很多变种，下面就介绍几种常用的方法。特别注意，仅当我们面对的是一个凸优化问题，梯度下降法才能够保证让我们找到全局最优解。

Batch Gradient Descent

批梯度下降法，其本质是每一轮迭代使用整个训练集去更新权重，即考虑了整体样本的梯度。其算法伪代码为：

$Repeat ;Until ;convergence; {$

$θ_{j} := θ_{j} + α \sum_{i = 1}^{m} (y^{(i)} - h_{θ} (x^{(i)})) x_{j}^{(i)};; (f o r; e v e r y; j)$

$Extra close brace or missing open brace$

Stochastic Gradient Descent

随机梯度下降法，其本质是每次迭代只用一个样例去计算梯度，更新参数。相比起批梯度下降法，随机梯度下降法大大提高了计算效率。从理论上说，SGD能让我们更快地找到最佳的参数，但是它有可能无法收敛到极小值，而是在极小值附近波动。但实际情况时，对于极小值附近的值也是对极小值的一个很好的近似，因此在数据集较大的情况下，SGD的实际效果是优于BGD的。其算法伪代码为：

$Loop ; {$

$ \quad for ;i=1 ;to;m, ; {$

$θ_{j} := θ_{j} + α (y^{(i)} - h_{θ} (x^{(i)})) x_{j}^{(i)};; (f o r; e v e r y; j)$

$Extra close brace or missing open brace$

实例

我们以拟合一条直线作为例子，以下给出一些前提定义：

训练样例 $X_{i} (a_{i}, b_{i})$ ， $i = 1, 2, \dots, n$ ， $n$ 为样本大小
导师信号 $D = [d_{1}, d_{1}, \dots, d_{i}]$ ， $i = 1, 2, \dots, n$ ， $n$ 为样本大小
$h (X_{i})$ 是在假设 $h$ 下预测得到的预测值
权值矩阵 $W = [w_{0}, w_{1}]$
目标函数 $w_{0} x + w_{1} y$
学习率（步长） $η$ 4， $0 < η < 1$
更新法则： $W (n + 1) = W (n) + η * X_{i} * (d_{i} - h (X_{i}))$

我们输入的数据是一系列的点，以及导师信号D（target value）。我们期望的输出是描述这个直线的权值矩阵 $W = [w_{0}, w_{1}]$ 。

初始化变量

初始化一些变量，其含义注释有描述。

import numpy as np
a = 0.1 # 0 < a < 1
X = np.array([[-1, 1], [-1, 0], [0, 1], [0, 0]]) # Input matrix
D = np.array([1, 1, 1, 0]) # target value
W = np.array([0, 0]) # Weight vector
expect_e = 0.005 # Expected Error
maxtrycount = 20

激活函数

激活函数（Activation Function）可以视为一个神经元对输入的反馈。举个简单的例子来帮助大家理解，我们听到一个消息，可能会激动，也可能不会激动。这个激活函数就是来判断我们是否会激动的函数。具体看，假如我们得知的是考试分数，80分以下我们就不会激动，80分以上我们就激动，那么这个激活函数就可以写为：

def sgn(x):
	if x > 80:
	   激动
	else:
	   不激动

那么在我们这个例子中，我们要确定一条直线，那么我们给出的是这个点在线的上方（1）还是下方（0）。

# Activation Function
def sgn(v):
  if v > 0:
    return 1
  else:
    return 0

输出信号

在每一个神经元我们要输出预测值，这是根据上面给出的激活函数得出的。

def get_v(W, x):
  return sgn(np.dot(W.T, x))

dot是矩阵乘法，W.T是代表W的转置。因此np.dot(W.T, x))是一个实数。

计算误差

误差是预测值与导师信号之差。

def get_error(W, x, d):
  return d - get_v(W, x)

更新权重

按照上面给出的权重更新公式来计算更新后的权重。

# Update Weights
'''
  W(n + 1) = W(n) + a * X(n) * e
'''
def getNewWeight(oldW, d, x, a):
  e = get_error(W, x, d)
  return (oldW + a * x * e, e)

返回一个pair，第一部分是更新后的参数，用于赋值给W，第二部分是当前这个样本 $X_{i}$ 的误差，用来计算均方。

训练过程

# Training
count = 0
while True:
  error = 0
  i = 0
  for xn in X:
    W, e = getNewWeight(W, D[i], xn, a)
    i += 1
    error += pow(e, 2) ## calculate MES
  error /= float(i)
  count += 1
  print(u"Weights after %d updates: " %count)
  print(W)

  print(u"Error: %f"%error)
  if error < expect_e or count >= maxtrycount:
    break

这里的训练过程我们称为批量的，因为每一个循环都对所有的样本进行训练，然后调整权重。这种做法开销比较大，但是精度较高。

测试部分

我们先对训练数据进行测试，然后再对两个单独的例子进行测试。

# Test
print("Begin Test")
test = np.array([2, 3])
print("X%s and W%s => %d"%(test, W.T, get_v(W, test)))
test = np.array([-2, -1])
print("X%s and W%s => %d"%(test, W.T, get_v(W, test)))

完整代码

'''
  Author: LeungYukshing
  Algorithm: Least Mean Squares
  observed is true value, predicted is predicted sample value
  MES = [(observed[0] - predicted[0]) * (observed[0] - predicted[0]) + ...
          + (observed[n] - predicted[n]) * (observed[n] - predicted[n])] / n
'''

'''
  UpperCase indicates a matrix or an array
  LowerCase indicates a value
'''

'''
  Learning Rate: a
  Too large: converge fastly, less stable
'''

import numpy as np
a = 0.1 # 0 < a < 1
X = np.array([[-1, 1], [-1, 0], [0, 1], [0, 0]]) # Input matrix
D = np.array([1, 1, 1, 0]) # target value
W = np.array([0, 0]) # Weight vector
expect_e = 0.005 # Expected Error
maxtrycount = 20

# Activation Function
def sgn(v):
  if v > 0:
    return 1
  else:
    return 0

def get_v(W, x):
  return sgn(np.dot(W.T, x))

def get_error(W, x, d):
  return d - get_v(W, x)

# Update Weights
'''
  W(n + 1) = W(n) + a * X(n) * e
'''
def getNewWeight(oldW, d, x, a):
  e = get_error(W, x, d)
  return (oldW + a * x * e, e)

# Training
count = 0
while True:
  error = 0
  i = 0
  for xn in X:
    W, e = getNewWeight(W, D[i], xn, a)
    i += 1
    error += pow(e, 2) ## calculate MES
  error /= float(i)
  count += 1
  print(u"Weights after %d updates: " %count)
  print(W)

  print(u"Error: %f"%error)
  if error < expect_e or count >= maxtrycount:
    break

print("Final Weight: ", W.T)

# Output
for xn in X:
  print("Xn%s and W%s =>%d"%(xn, W.T, get_v(W, xn)))

# Test
print("Begin Test")
test = np.array([2, 3])
print("X%s and W%s => %d"%(test, W.T, get_v(W, test)))
test = np.array([-2, -1])
print("X%s and W%s => %d"%(test, W.T, get_v(W, test)))

分析

先给出程序运行结果：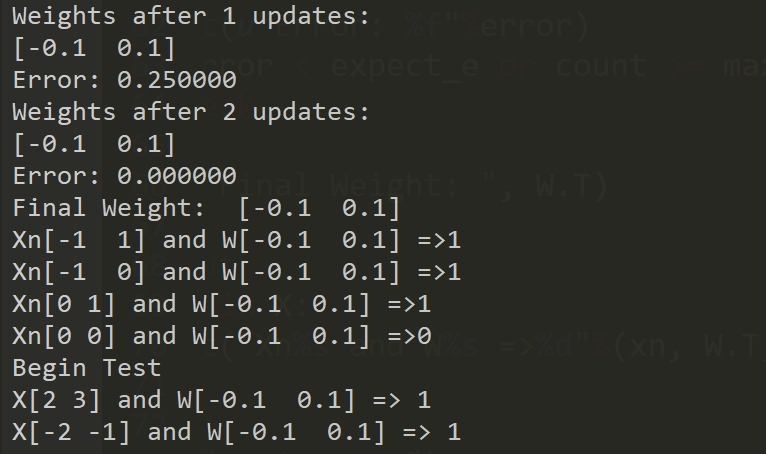

可以看出，实际上我们训练出来的直线是y=x。从拟合的角度看，我们根据给出的一系列点，最后拟合出一条直线。从分类的角度看，这条直线将二维平面分成两部分，在直线上方的标记为1，在直线下方的标记为0。

在这个例子中，训练两次后就已经满足了我们期望的误差，这是因为我给出的点是比较好的，很容易识别出来。对于其他的直线和数据集，可能需要多次的训练才能得到结果。

总结

LMS算法本质上是给我们提供了一种判断方法，判断当前的权值对于实际预测的准确性。机器学习的任务就是去极小化这个误差。先来看看这里用到的更新方法： $W (n + 1) = W (n) + η * X_{i} * (d_{i} - h (X_{i}))$

我们这样理解：

当 $(d_{i} - h (X_{i})) = 0$ 时，权值不会改变。这说明当导师信号和我们预测的信号一致时，我们就认为当前的分类是正确的，无需做出改变。
当 $(d_{i} - h (X_{i}))$ 为正时，说明预测值比导师信号要小，所以需要在原权值的基础上增加一定的比例。反之亦然。
当 $X_{i} = 0$ 时，权值不会改变。这说明当这个特征 $X_{i}$ 没有出现时，它的权值是不会因为误差而改变的。

当然，在实际应用中，我们更多使用的是梯度下降法，这会在之后的博客中和大家分享，这里就只分析LMS算法。谢谢您的支持！